Notes on Lambda Calculus
Categories:
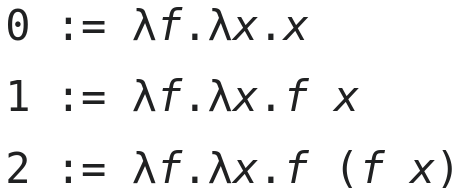
Church encoding of the natural numbers in lambda calculus
Notes on Lambda Calculus
Passive-Interface-Pair-for-Decentralized-Identity-DID
In response to Marta’s (N+Fold) discussion on Comparing Interoperability when there is a transliteration of material forms. in relation to her Project Catalyst Fund 6 proposal Passive-Interface-Pair-for-Decentralized-Identity-DID I touched upon the subject of Lambda Calculus :
It was an interesting session. With reference to your wiki notes: yes “Laws of Form” looks like it has parallels with Lambda Calculus. The name I was searching for on Saturday was Alonzo Church who collaborated with Alan Turing on computability. And Church’s Lambda Calculus came to mind, in relation to your proposal, because it is an analogue means of computation (written notation) and a way to test what is computable without a digital computer. Another aspect of Lambda Calculus is its sparseness - at its core it is a non-extensional theory of functions. So it does not rely on external references to ordered pairs of data. Lambda functions are unary and immutable. A passive interface with an immutable history if it is computable would be a Turing machine and a possible reader/writer could be Lambda functions. Discord link
Mapping Multiple Traces of Immutability. Why?
This comment was discussed further in an After Town Hall session hosted by Marta on 22nd September 2021 entitled “Mapping Multiple Traces of Immutability. Why?" and recorded on YouTube.
There was some discussion over the statement “A passive interface with an immutable history if it is computable would be a Turing machine and a possible reader/writer could be Lambda functions.”. Filip understood that this was simply meant as a general statement. SofiH picked up that what is computable is Turing complete. Lambda Calculus is just one means to express what is computable. As per the Church-Turing Thesis. The focus in Lambda is to do this through the use of functional reduction and I wanted to draw attention to a way of thinking abstractly about computation where the use of functional reduction is made explicit. In essence, to compute is to be able to solve numerical functions.
Extensional versus intensional Functions
Extensional
An extensional mapping of an input onto an output renders the input \(X\) & output \(Y\) as a domain \(X\) & co-domain \(Y\).
A function in this context \(f : X \to Y\) is a set of pairs \(f \subseteq X \times Y\) such that for each \(x \in X\), there exists exactly one \(y \in Y\) such that \((x,y) \in f\).
intensional
Beyond Lambda Calculus
A further development is process calculi such as π-calculus which extend functional reduction to concurrent systems.
A succent explanantion of the intensional nature of Lambda Calculus is given by Peter Selinger in his Lecture Notes on the Lambda Calculus .
Think of a computer program as defining a function that maps onput to output. Most computer programmers (and users) do not only care about the extensional behavior of a program (which inputs are mapped to which outputs), but also about how the output is calculated: How much time does it take? How much memory and disk space is used in the process? How much communication bandwidth is used? These are intensional questions having to do with the particular way in which a function was defined.